Lab Logo

  Advanced Computing and EDA (ACE) Lab at SJTU
HomePeopleResearchPublicationsTeachingActivitiesCodes & Links

Approximate Computing
Three important goals of VLSI design are reducing circuit area, improving circuit frequency, and reducing power consumption, all of which are achieved under the basic assumption that the circuit correctly implements the specified function. However, many applications widely used today, such as signal processing, pattern recognition, and machine learning, do not require perfect computation. Instead, results with small errors are still acceptable. A new design paradigm, known as approximate computing, is recently proposed to design circuits for those error-tolerant applications. Exploiting the error tolerance of applications, it deliberately sacrifices a small amount of accuracy to achieve improvement in area, performance, and power consumption.

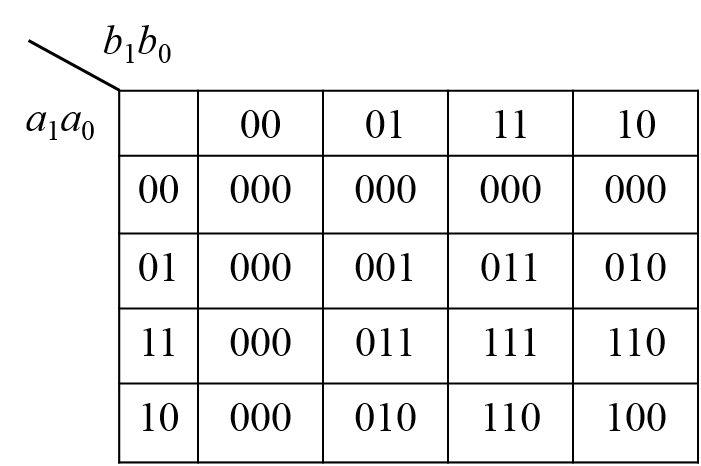
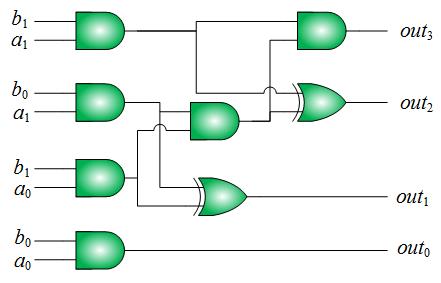
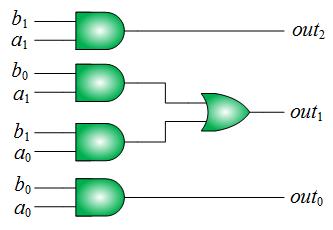
An example of approximate computing is shown in Fig. 1. Fig. 1(a) shows the Karnaugh map of an accurate 2-bit multiplier. If we change the output "1001" in the red circle in Fig. 1(a) to "111", we obtain the Karnaugh map of an approximate 2-bit multiplier, as shown in Fig. 1(b). The circuit for the accurate multiplier and that for the approximate multiplier are shown in Fig. 1(c) and 1(d), respectively. Notice that by introducing a small amount of inaccuracy, we reduce both the area and the delay of the original multiplier significantly.
Original Karnaugh Map

(a) Karnaugh map of accurate multiplier

 Approximate Karnaugh Map

(b) Karnaugh map of approximate multiplier
Accurate Multiplier
(c) Circuit of accurate multiplier
Approximate Multiplier

(d) Circuit of approximate multiplier

Fig. 1. Accurate and approximate designs of 2-bit multiplier from the paper "Trading accuracy for power with an underdesigned multiplier architecture" by Kulkarni et al., 2011.

We study the following fundamental problems related to approximate computing:
  1. Approximate logic synthesis. We develop algorithms to automatically synthesize approximate circuits. Specifically, given a target function and an error specification, the algorithm will produce an optimal circuit which is an approximation to the target function satisfying the error specification.
  2. The design, synthesis, and analysis of approximate arithmetic circuits. Arithmetic circuits, including adders and multipliers, are key building blocks of many applications. We study how to design and synthesize high-performance energy-efficient approximate adders and multipliers by deliberately introducing errors. We also study how to analyze the error of these approximate circuits.
  3. The design of approximate computing architectures. We study how to design novel architectures exploiting approximate computing to improve energy efficiency.

Selected Publications on Approximate Logic Synthesis

Selected Publications on the Design, Synthesis, and Analysis of Approximate Arithmetic Circuits

Selected Publications on the Design of Approximate Computing Architectures


Stochastic Computing
Traditional arithmetic circuits operate on numbers encoded by binary radix, which is a deterministic way to represent numerical values with zeros and ones. Fundamentally different from the binary radix, stochastic encoding is another way to represent numerical values by logical zeros and ones.  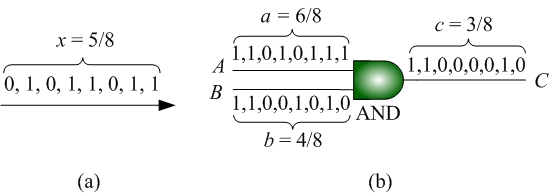In such a encoding, a real value p in the unit interval is represented by a sequence of N random bits X1, X2, ..., XN, with each Xi having probability p of being one and probability (1-p) of being zero, i.e., P(Xi = 1) = p and P(Xi = 0) = 1-p. Fig. 2(a) shows an example of a stochastic bit stream encoding the value 5/8.

Since the random sequences are composed of binary digits, we can apply digital circuits to process them. Thus, instead of mapping Boolean values into Boolean values, a digital circuit now maps real probability values into real probability values. We refer to this type of computation as stochastic computing. Fig. 2(b) illustrates an AND gate performing multiplication on stochastic bit streams.

Stochastic Encoding and Circuit
Fig. 2. Stochastic encoding and computation on stochastic encoding: (a) A stochastic bit stream encoding the value x = 5/8; (b) An AND gate multiplying two values encoded by two input stochastic bit streams.

We study the following fundamental problems related to stochastic computing:
  1. The synthesis of stochastic computing circuits. In the earlier works on stochastic computing, a number of stochastic circuits are designed manually, but they are restricted to basic computation units such as adder and multiplier. We explore algorithms to automatically synthesize stochastic circuits for arbitrary arithmetic functions.
  2. The generation of stochastic bit streams. Stochastic computing relies on stochastic number generators (SNGs) to generate input stochastic bit streams of the desired probabilities. However, they need far more area and power consumption than the stochastic computing core, offsetting the latter's advantage. We explore solutions to reduce the area and power consumption of SNGs.
  3. Architectures and application of stochastic computing. We explore architecture for stochastic computing. We apply such computational paradigm to different applications, such as image processing and numerical integration.

Selected Publications on the Synthesis of Stochastic Computing Circuits

Selected Publications on the Generation of Stochastic Bit Streams

Selected Publications on Architectures and Applications of Stochastic Computing


In-Memory Computing
Traditional von Neumann architecture requires data movement between the processor and the memory, which causes a bottleneck in performance and energy efficiency known as the "memory wall". To address this problem, in-memory computing (IMC) paradigm has been proposed. It explores opportunities to compute within the memory so that the amount of data movement can be significantly reduced. We study the following topics related to IMC:
  1. Hardware/software co-design for reliable analog IMC. Analog IMC, e.g., those based on resistive random-access memory (RRAM), is a promising choice for realizing neural network (NN) accelerators, as it enables efficient vector-matrix multiplication, a dominant operation of NNs. However, a big challenge is that the resistance variation caused by the device non-idealities of these analog IMC degrades the NN accuracy. We study hardware/software co-design to mitigate the reliability issue of analog IMC.
  2. Synthesis and scheduling for digital IMC. Digital IMC is also an important IMC design style. A digital IMC architecture typically supports a few primitive logic operations such as XOR and majority operations, and it performs a complicated computation by decomposing the target computation into a sequence of these primitive operations. Given a target computation, we study how to synthesize an optimized sequence of the primitive operations and then schedule the sequence to realize the target computation.

Selected Publications on Hardware/Software Co-Design for Reliable Analog IMC

Selected Publications on Synthesis and Scheduling for Digital IMC


Electronic Design Automation for VLSI
We are also interested in electronic design automation (EDA) for VLSI. Topics include:
  1. Logic synthesis: Logic synthesis is an important step in EDA. It takes a circuit netlist as input and returns a simplified one. However, obtaining the optimal netlist is a computationally intractable problem. In this direction, we explore various novel angles to advance the state-of-the-art logic synthesis methods.
  2. High-level synthesis: High-level synthesis (HLS) is a technique that enables designers to automatically convert a program written in high-level language (such as C, C++, and Python) into a description in hardware-description language (such as Verilog and VHDL). It significantly enhances the hardware development efficiency and allows more people (including those with little knowledge of hardware) to build hardwares to accelerate their applications. In this direction, we explore various novel angles to improve the existing HLS methods.
  3. Arithmetic circuit synthesis: Arithmetic circuits, such as adders and multipliers, are important building blocks of many applications. In this direction, we develop algorithms to synthesize optimized arithmetic circuits.
  4. Standard cell synthesis: Standard cells are basic building blocks of modern integrated circuits. The area, delay, and power consumption of a circuit highly depend on the available standard cells. In this direction, on the one hand, we explore methods to automatically identify Boolean functions for which it is worth to build standard cells. On the other hand, we develop algorithms to synthesize an optimized standard cell for a given Boolean function.
  5. Circuit analysis: When designing a circuit, we usually want to analyze its area, delay, power consumption, etc. For large-scale circuits, we require such analysis to be efficient yet accurate. In this direction, we develop algorithms to efficiently and accurately analyze circuits for the metrics of interest.

Selected Publications